Research Interests:
I am Associate Professor in the Granular Matter group in the Faculty of Thermal and Fluid Engineering, which is part of Department of Engineering Technology and the Institute for Nanotechnology MESA+, at the University of Twente. I lead the subgroup on Virtual Prototyping of Granular Processes.
I develop models and algorithms capable of predicting the behaviour of complex multi-physics systems on different scales. Specifically, I have extensive experience in modelling particulate materials, varying in size from nanometres (molecules) to micrometres (food/pharma/3D printing powders), millimetres (sand/soil) or meters (rocks). I have multi-disciplinary interests in this line of research, from numerical solvers, analytical modelling and granular physics to engineering applications.
I have developed microscopic contact models for frictional, wetted and sintered particles, as well as rheological laws for granular and atomistic flows and mixtures. My students work on applying these models to avalanche flows, 3D printing, tableting, extrusion, and many other applications.
I have cofounded and am the lead lead developer of MercuryDPM, an open-source software for discrete particle simulations. I further developed MercuryCG, an accurate and efficient technique to extract physically meaningful quantities from discrete particle simulations (or experiments), and to couple particle and continuum simulations. It is now part of MercuryDPM. I implemented a finite element solver and developed error estimators for hp-adaptive mesh refinement. I developed Moomph, a versatile solver capable of addressing coupled multiscale, multiphysics problems,
MercuryDPM has unique features specifically developed to allow the simulation of real machinery, which has led to several industrial collaborations. For experimental validation and calibration, I have developed close collaborations with several external partners.
For more details and publications, see:
- Contact modelling
- Experimental validation
- Multiscale models for particulates
- Finite Element analysis
- Industrial applications
Students:
Current students:
Graduated students:
- Remco Hartkamp
- Olukayode Imole
- Deepak Tunuguntla
- Sudeshna Roy
- Hao Shi
- Marnix van Schrojenstein Lantman
- Irana Dennissen
- Juan Alvarez
News:

In 2018, I have obtained a prestigious NWO-VIDI grant, allowing me to develop a new and exciting approach to particulate process design: Virtual Prototyping. Please apply here.
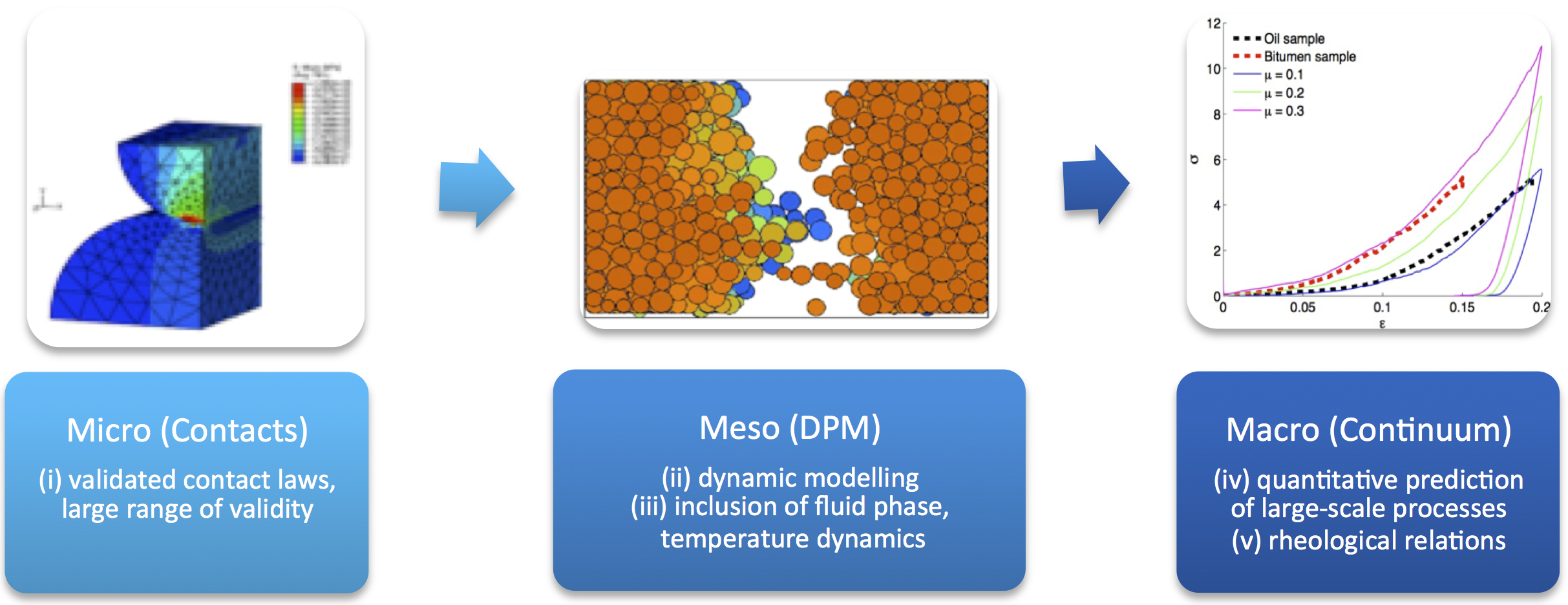
In 2017, I have started a new research line on modelling agglomeration processes (tabletting and sintering) of particulate materials. Agglomerates will be modelled using a mesoscale approach.
MercuryDPM is available here. New features: More complex shapes and Lees-Edwards boundaries; reorganisation of the source files; and a better build system (cmake). Have fun with it, and, as always, give us feedback!

The University of Twente will proudly host the 8th conference on Discrete Element Methods in August 2019. I am co-organising the event with Anthony Thornton, Stefan Luding, and Donna Fitzsimmons.
MercuryLab offers popular courses on C++ programming and Discrete Particle Simulations. More information can be found here.

"Transport Phenomena" (Module 6), of which I am teaching "Numerical Methods", was recognized/ rewarded as the best TOM module in Chemical Engineering in 2018. Furthermore, the Keuzegids Universiteiten has appointed the Chemical Engineering bachelor's programme a "Top rated programme" for the fifth consecutive year. Time to celebrate!


