Finite Element Analysis for Particulate Materials
Continuum methods model can be used to model particulate material as a continuous mass, rather than discrete particles. The material behaviour is thus described by differential equations that are based on the conservation of mass, momentum, and energy. Information about the particular material is added via constitutive relations. These equations are then discretised and solved, e.g. via the Finite Element Method (FEM).
Continuum methods are efficient methods to simulate large, industrial-scale machinery. However, unlike for fluids and solids, no general constitutive relations exist for particulates. Thus, all available constitutive models are based on simplifying assumptions that limit their accuracy and hence range of applicability.
During my PhD, I have implemented an FEM solver for transport phenomena and applied it to acoustic, magnetic, and shallow-water waves [J1,J2,J11,T1]. I am now supervising two PhD projects that use oomph-lib to simulate wetted particulates under shear and shallow particulate flows.
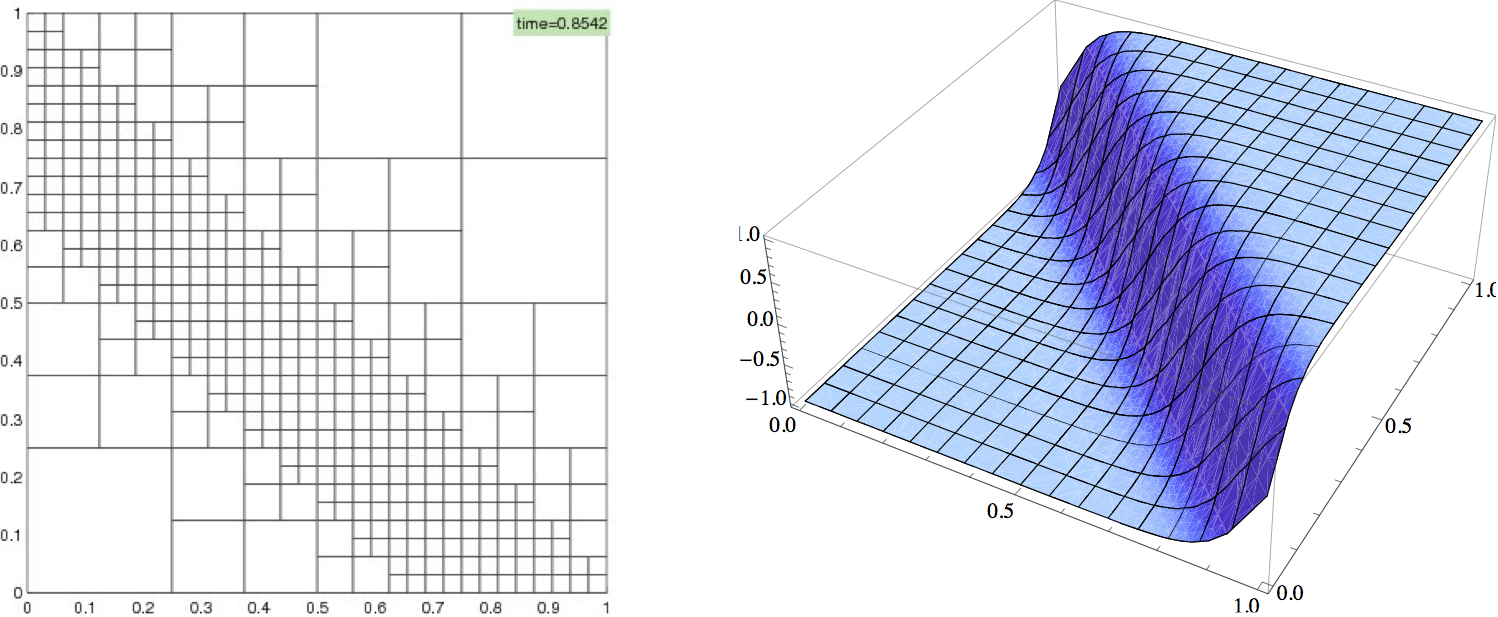
A posteriori error estimates are a useful tool to verify the quality of finite element approximations and to control the error in adaptive meshes. We apply the discontinuous Galerkin method to first-order linear hyperbolic systems in two and three space dimensions. We explicitly write down the leading error term and solve local finite element problems to obtain a posteriori error estimates. We present convergence and numerical results for problems from acoustics and electromagnetism [J1,J2,J11,T1].
As part of the PhD project of M van Schroeienstein Lantman, we apply an extended rheology for quasistatic particulate shear flows [J14,C5,C4,O5], where the inertial μ(I)-rheology is extended to account for pressure, gravity, and cohesion effects as well. This work is still in progress, but look out for publications on that topic in the near future.
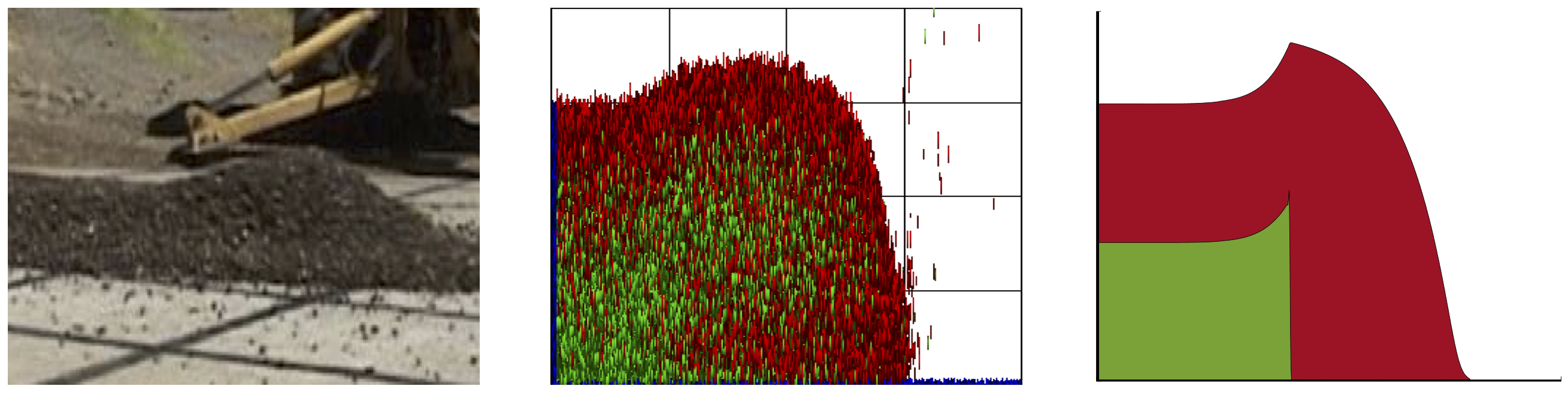
Predicting the behaviour of hazardous natural particulate flows (e.g. snow slab avalanches, debris- flows and pyroclastic flows) is vital for an accurate assessment of the risks posed by such events. The main features of such flows can be predicted by simple depth-averaged models for shallow particulate chute flows, validated by DPM simulations [J3,J4,S4]. In the PhD project of I Denissen, we use this model to predict the shape of the avalanche head. She is now extending this model to account for segregation as well [A5]. Simultaneously, D Tunuguntla is looking at the flow through a contraction [in prep].