How to use this documentation
Information for users of this application
General Information
This code is written in C++ and does make use of both templates and the object oriented nature of C++. This basic architecture is to have a core kernel code (located in scr) that is general and flexible and then very small driver codes (located in DRIVERS) that pick out the parts of the kernel required to solve specific problems.
Introduction to the Code
How to use this documentation
Information for users of this application
General Information
This code is written in C++ and does make use of both templates and the object oriented nature of C++. This basic architecture is to have a core kernel code (located in scr) that is general and flexible and then very small driver codes (located in DRIVERS) that pick out the parts of the kernel required to solve specific problems.
Directory Structure
At the top level you will find three main directories
DRIVERS/
scr/
DOCUMENTATION/
In the DOCUMENTATION direction is located the documentation, i.e. this file. Please note, if you find no documentation there it can be generated by going into the DRIVERS/ direction and typing "make doc". If the documentation becomes corrupt the following will force it to regenerate "make doc_clean; make doc"
The scr direction contains the heart of the code and as a users you should not need to known much about it.
The DRIVERS directory has a series of subdirectories for example Simple_MD/ that each contain a series of demo codes illustrating how to use the main src code. Typing "make selftest" in the top level of drivers would perform checks on all parts of the code to confirm everything is functioning as intended.
In each subdirectory (e.g. Simple_MD) there is a makefile that can be used to compile the individual codes. Note typing "make selftest" at this level will perform the test for that section of the code only. Also in subdirectory they is a second subdirectory call run/. If you move in this directory from here any driver can be run with the command "sc/quick_run driver_name". This command will compile and run driver_name.
Finally running a code will (in general) generate three files called some_name.data, some_name.disp and some_name.stat. The files with .data extension contain all the position and velocity information for every particles. The .stat extension, contains macroscopic statistics about the problem (the information contained is semi-driver dependent). Finally .disp extension is an a script file that to run to plot for .data output file using xballs.
The Scripts
Along with this code you will find a directory called scripts. This contains a number of bash scripts designed to work with both the MD and finite volume programs. A brief summary of each script is as follows
- clean_run : The code has a feature to automatically number your runs (not yet documents, see parm_demo code for how to use). So the first time you run the code will be labelled 1, second 2, etc... Running clean_run CODENAME RUN_NUM will delete all files with run number RUN_NUM of driver code CODENAME. This does not prompt for each file, so please be careful with this command.
- fstat : To be documented
- go_run : This is internal script used by run and should not be called directly
- renumber_run : This changes the number of previous run. renumber_run CODENAME OLD_NUM NEW_NUM will change the number of all files associated with CODENAME run number OLD_NUM to be associated with run NEW_NUM. Please note again this command does not check it NEW_RUN exists so will delete any existing data associated with NEW_RUN.
- self_test : This is the script which does the work for 'make selftest'. It should never be called directly, please use make selftest.
- enestatistics : To be documented
- fstatatistics : To be documented
- kill_all : This kills all copies of a code running on a cluster. To use this commands please type the list of machine names on your cluster in the list filed at the top. Note the default list is more machine in the MSM group at the University of Twente
- report : This is the script which does the work of 'make report', please use make report instead of this command directly.
- find_code : This reports all codes belonging to your on your cluster, please again in this script you have to list the machine names of your cluster
- go_find_machine : Looks for spare ca[capacity on your cluster. To use this script please enter you machine list in list and the maxload per machine in maxload.
- make_movie : This script uses xball to make a movie. The command is called with make_movie SOMEFILE.disp, this will make a movie of the xballs output normally generated by the disp file SOMEFILE.disp.
- run : run MY_CODE will make and run the code called MY_CODE. This automatically looks for free space on your cluster using the information defined in go_find_machine
- fpdiff.py : Calculated the floating point different between number in text file. This is part of the internal working of the selftest routire. This original version of this code was created for the oomph-lib project at the University of Manchester.
- go_make : This is internal script used by run.
- quick_run : Same as run, but runs the code on the local machine.
Creating your own DRIVERS directory for your code
It you look in the DRIVERS directory you will see several subdirectories. These subdirectories contain collections of similar codes and, as a new user, you probably want to create a new directory for your own driver codes. To do this copy the TEMPLATE direction to you YOUR_DIR_NAME (if your are a developer and have access to svn repository it is advisable to svn copy to create your new DRIVERS directory)
Information for developers of this application
Variables and Equations
- global parameters: for details refer to MD class documentation.
- time domain
![$[0,t_{\mbox{max}}]$](form_0.png) ,
,
- spatial domain
![$[x_{\mbox{min}},x_{\mbox{max}}] \times [y_{\mbox{min}},y_{\mbox{max}}] \times [z_{\mbox{min}},z_{\mbox{max}}]$](form_1.png) ,
,
- number of particles
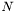 ,
,
- number of (regular) walls
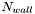 ,
,
- number of periodic walls
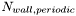
- gravitational acceleration
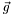 ,
,
- Walls are defined by outward unit normal
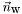 and position
and position 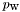 :
: 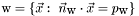
- global variables: for details refer to MD class documentation.
- time
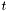 ,
,
- parameters for particle
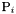 : for details refer to CParticle class documentation
: for details refer to CParticle class documentation
- radius
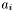 ,
,
- mass
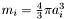 ,
,
- inertia
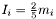 ,
,
- normal spring constant
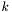 (globally set)
(globally set)
- normal dissipation coefficient
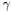 ,
,
- tangential dissipation coefficient
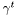 ,
,
- Coulomb friction coefficient
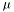
- variables for particle
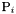 : for details refer to CParticle class documentation
: for details refer to CParticle class documentation
- position
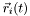 ,
,
- velocity
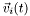 ,
,
- angle
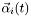 ,
,
- angular velocity
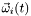 .
.
- initial values:
- position
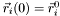 ,
,
- velocity
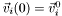 ,
,
- angle
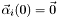 ,
,
- angular velocity
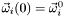 .
.
- variables for each collision between particles
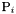 and
and 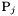 :
:
- relative position
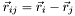 ,
,
- normal direction
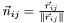 ,
,
- overlap
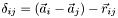 ,
,
- relative velocity
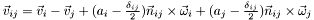
- relative normal velocity
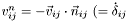 ),
),
- normal force (spring-dashpot model)
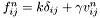 ,
,
- relative tangential velocity
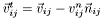 ,
,
- tangential direction
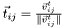 ,
,
- tangential force (sliding friction model)
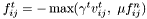 ,
,
- collision force
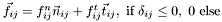 ,
,
- Variables for collisions between particle
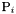 and wall
and wall 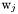 :
:
- normal direction
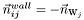 ,
,
- overlap
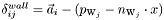 ,
,
- relative velocity
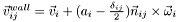 ,
,
- all else is the same as for particle collisions
- Force and torque calculations
![\[ \vec{f}_i = m_i \vec{g} + \sum_{j=1}^N \vec{f}_{ij} + \sum_{j=1}^{N_{wall}} \vec{f}_{ij}^{wall}, \]](form_42.png)
![\[ \vec{t}_i = \sum_{j=1}^N (a_i-\frac{\delta_{ij}}{2}) \vec{n}_{ij} \times \vec{f}_{ij} + \sum_{j=1}^{N_{wall}} (a_i-\frac{\delta_{ij}^{wall}}{2}) \vec{n}_{ij}^{wall} \times \vec{f}_{ij}^{wall}. \]](form_43.png)
- Time integration
![\[ \vec{\dot{r}}_i = \vec{v}_i,\ m_i \vec{\dot{v}}_i = \vec{f}_i,\quad \vec{\dot{\alpha}}_i = \vec{\omega}_i,\ I_i \vec{\dot{\omega}}_i = \vec{t}_i \]](form_44.png)
Implementation
Time Stepping
Verlet integration for 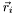 , forward Euler for
, forward Euler for 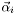 ,
, 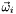 , fixed time step
, fixed time step 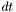 .
.
![$[0,t_{\mbox{max}}]$](form_0.png) ,
,![$[x_{\mbox{min}},x_{\mbox{max}}] \times [y_{\mbox{min}},y_{\mbox{max}}] \times [z_{\mbox{min}},z_{\mbox{max}}]$](form_1.png) ,
,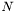 ,
,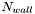 ,
,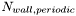
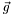 ,
,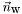 and position
and position 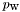 :
: 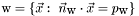
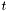 ,
,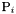 : for details refer to CParticle class documentation
: for details refer to CParticle class documentation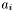 ,
,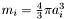 ,
,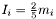 ,
,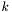 (globally set)
(globally set)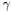 ,
,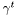 ,
,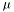
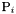 : for details refer to CParticle class documentation
: for details refer to CParticle class documentation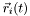 ,
,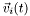 ,
,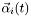 ,
,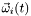 .
.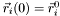 ,
,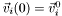 ,
,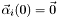 ,
,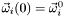 .
.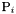 and
and 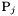 :
: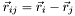 ,
,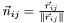 ,
,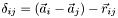 ,
,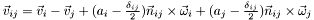
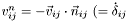 ),
),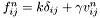 ,
,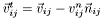 ,
,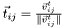 ,
,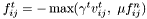 ,
,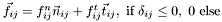 ,
,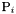 and wall
and wall 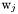 :
: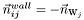 ,
,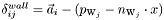 ,
,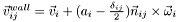 ,
,![\[ \vec{f}_i = m_i \vec{g} + \sum_{j=1}^N \vec{f}_{ij} + \sum_{j=1}^{N_{wall}} \vec{f}_{ij}^{wall}, \]](form_42.png)
![\[ \vec{t}_i = \sum_{j=1}^N (a_i-\frac{\delta_{ij}}{2}) \vec{n}_{ij} \times \vec{f}_{ij} + \sum_{j=1}^{N_{wall}} (a_i-\frac{\delta_{ij}^{wall}}{2}) \vec{n}_{ij}^{wall} \times \vec{f}_{ij}^{wall}. \]](form_43.png)
![\[ \vec{\dot{r}}_i = \vec{v}_i,\ m_i \vec{\dot{v}}_i = \vec{f}_i,\quad \vec{\dot{\alpha}}_i = \vec{\omega}_i,\ I_i \vec{\dot{\omega}}_i = \vec{t}_i \]](form_44.png)
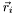 , forward Euler for
, forward Euler for 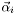 ,
, 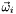 , fixed time step
, fixed time step 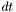 .
.  1.7.6.1
1.7.6.1