HG-MD  1
Public Member Functions | Static Public Member Functions | Public Attributes | Private Attributes | Static Private Attributes | Friends
StatisticsPoint< T > Struct Template Reference

This class stores statistical values for a given spatial position; to be used in combination with StatisticsVector. More...

#include <StatisticsPoint.h>

Collaboration diagram for StatisticsPoint< T >:
Collaboration graph
[legend]

List of all members.

Public Member Functions

 StatisticsPoint ()
 Constructor sets sensible values.
 StatisticsPoint (const StatisticsPoint &other)
 Copy constructor; simply copies everything.
void set_CG_type (const char *CG_type)
 see StatisticsVector::set_CG_type
CG get_CG_type () const
 see StatisticsVector::get_CG_type
void set_w2 (Mdouble new_)
 see StatisticsVector::set_w2
Mdouble get_w2 () const
 see StatisticsVector::get_w2
Mdouble get_w () const
 see StatisticsVector::get_w
Mdouble get_cutoff ()
 see StatisticsVector::get_cutoff
Mdouble get_cutoff2 ()
 see StatisticsVector::get_cutoff2
Mdouble get_xmaxStat ()
 see StatisticsVector::get_xmaxStat
Mdouble get_ymaxStat ()
 see StatisticsVector::get_ymaxStat
Mdouble get_zmaxStat ()
 see StatisticsVector::get_zmaxStat
Mdouble get_xminStat ()
 see StatisticsVector::get_xminStat
Mdouble get_yminStat ()
 see StatisticsVector::get_yminStat
Mdouble get_zminStat ()
 see StatisticsVector::get_zminStat
void get_n (int &nx_, int &ny_, int &nz_)
 see StatisticsVector::get_n
Mdouble evaluatePolynomial (Mdouble r)
 see StatisticsVector::evaluatePolynomial
Mdouble evaluateIntegral (Mdouble n1, Mdouble n2, Mdouble t)
 see StatisticsVector::evaluateIntegral
void set_CG_invvolume ()
 sets CG_invvolume
Mdouble get_CG_invvolume ()
 returns CG_invvolume
void set_Gaussian_invvolume (int dim)
 sets CG_invvolume if CG_type=Gaussian
void set_Heaviside_invvolume ()
 sets CG_invvolume if CG_type=HeaviSideSphere
void set_Polynomial_invvolume (int dim)
 sets CG_invvolume if CG_type=Polynomial
void set_Position (Vec3D new_)
 sets Position
Vec3D get_Position () const
 returns Position
void set_zero ()
 Sets all statistical variables to zero.
StatisticsPoint< T > getSquared ()
 Squares all statistical variables; needed for variance.
StatisticsPoint< T > & operator= (const StatisticsPoint< T > &P)
 Defines a equal operator needed for copy constructor.
StatisticsPoint< T > & operator+= (const StatisticsPoint< T > &P)
 Defines a plus operator needed to average values ( 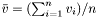$ \bar{v} = (\sum_{i=1}^n v_i)/n $ )
StatisticsPoint< T > & operator-= (const StatisticsPoint< T > &P)
 Defines a plus operator needed to calculate variance.
StatisticsPoint< T > & operator/= (const Mdouble a)
 Defines a division operator needed to average values ( 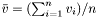$ \bar{v} = (\sum_{i=1}^n v_i)/n $ )
void timeAverage (const int n)
 Defines a division operator needed to time-average values (because the displacement does not have a value at the first timestep, this is slightly different than /=)
Mdouble get_distance2 (Vec3D &P)
 returns the coarse graining distance in the coordinates that are not averaged about
Mdouble dot (Vec3D &P, Vec3D &Q)
 Returns the dot product of two vectors in the coordinates that are not averaged about.
Mdouble CG_function (Vec3D &PI)
 Returns the value of the course graining function phi(P,PI)
Mdouble CG_function_2D (Vec3D &PI)
 returns the value of the course graining function phi(P,PI) averaged along a line
Mdouble CG_function_1D (Vec3D &PI)
 Returns the value of the course graining function phi(P,PI) averaged along a plane.
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
 gradient of phi
Vec3D CG_integral_gradient (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal)
 gradient of phi
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
 Returns the value of the coarse graining integral 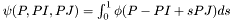$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $.
Mdouble CG_integral_2D (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
 Returns the value of the coarse graining integral 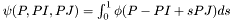$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $ averaged along a line.
Mdouble CG_integral_3D (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
Mdouble CG_integral_1D (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
 Returns the value of the coarse graining integral 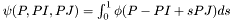$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $ averaged along a plane.
string print () const
 Outputs statistical variables in human-readable format.
string print_sqrt () const
 Outputs root of statistical variables in human-readable format.
string write_variable_names ()
 Outputs names of statistical variables in computer-readable format.
string write () const
 Outputs statistical variables in computer-readable format.
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
void set_CG_invvolume ()
template<>
Mdouble CG_function (Vec3D &PI)
template<>
Mdouble CG_function (Vec3D &PI)
template<>
Mdouble CG_function (Vec3D &PI)
template<>
Mdouble CG_function (Vec3D &PI)
template<>
Mdouble CG_function (Vec3D &PI)
template<>
Mdouble CG_function (Vec3D &PI)
template<>
double CG_function (Vec3D &)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &P, Mdouble phi)
template<>
Vec3D CG_gradient (Vec3D &, double)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
Mdouble CG_integral (Vec3D &P1, Vec3D &P2, Vec3D &P1_P2_normal, Mdouble P1_P2_distance)
template<>
double CG_integral (Vec3D &, Vec3D &, Vec3D &, double)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
Mdouble get_distance2 (Vec3D &P)
template<>
double get_distance2 (Vec3D &)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
Mdouble dot (Vec3D &P, Vec3D &Q)
template<>
double dot (Vec3D &, Vec3D &)

Static Public Member Functions

static void set_gb (StatisticsVector< T > *new_gb)
 see StatisticsVector::set_CG_type

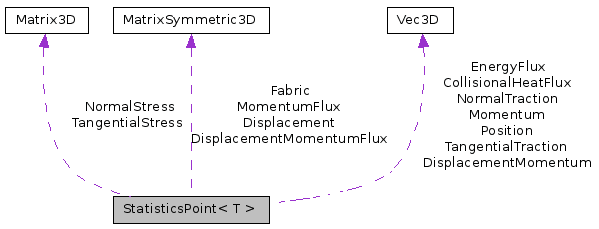
Public Attributes

Mdouble Nu
 Particle volume fraction, 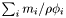$\sum_i m_i/\rho \phi_i$.
Mdouble Density
 Density, 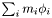$\sum_i m_i \phi_i$.
Vec3D Momentum
 Momentum, 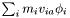$\sum_i m_i v_{ia} \phi_i$.
Vec3D DisplacementMomentum
 Momentum from linear displacement, 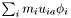$\sum_i m_i u_{ia} \phi_i$.
MatrixSymmetric3D Displacement
 Linear displacement, 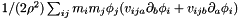$1/(2 \rho^2) \sum_{ij} m_i m_j \phi_j (v_{ija} \partial_b \phi_i + v_{ijb} \partial_a \phi_i) $.
MatrixSymmetric3D MomentumFlux
 Momentum flux, 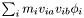$\sum_i m_i v_{ia} v_{ib} \phi_i$.
MatrixSymmetric3D DisplacementMomentumFlux
 Momentum flux from linear displacement, 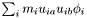$\sum_i m_i u_{ia} u_{ib} \phi_i$.
Vec3D EnergyFlux
 Energy flux, 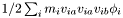$1/2 \sum_i m_i v_{ia} v_{ia} v_{ib} \phi_i$.
Matrix3D NormalStress
 Stress from normal forces, 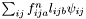$\sum_{ij} f^n_{ija} l_{ijb} \psi_{ij}$.
Matrix3D TangentialStress
 Stress from tangential forces, 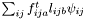$\sum_{ij} f^t_{ija} l_{ijb} \psi_{ij}$.
Vec3D NormalTraction
 Traction from normal forces, 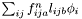$\sum_{ij} f^n_{ija} l_{ijb} \phi_i$.
Vec3D TangentialTraction
 Traction from tangential forces, 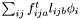$\sum_{ij} f^t_{ija} l_{ijb} \phi_i$.
MatrixSymmetric3D Fabric
 Fabric tensor, 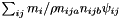$\sum_{ij} m_i/\rho n_{ija} n_{ijb} \psi_{ij}$.
Vec3D CollisionalHeatFlux
 Heat flux from collisions, 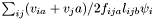$\sum_{ij} (v_{ia}+v_ja)/2 f_{ija} l_{ijb} \psi_i$.
Mdouble Dissipation
 Dissipation form collisions, 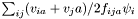$\sum_{ij} (v_{ia}+v_ja)/2 f_{ija} \psi_i$.
Mdouble Potential
 Elastic energy 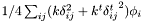$1/4 \sum_{ij} (k \delta_{ij}^2 +k^t {\delta^t_{ij}}^2) \phi_i$.
Mdouble CG_invvolume
 Prefactor of CG function which depends on $w.
int mirrorParticle
 indicates that a position is a (fake) particles used for periodic walls

Private Attributes

Vec3D Position
 Position at which evaluation occurs.

Static Private Attributes

static StatisticsVector< T > * gb
 Pointer to StatisticsVector (to obtain global parameters)

Friends

std::ostream & operator (std::ostream &os, const StatisticsPoint< T > &stat)
 Outputs statistical variables to ostream.

Detailed Description

template<StatType T>
struct StatisticsPoint< T >

This class stores statistical values for a given spatial position; to be used in combination with StatisticsVector.

Constructor & Destructor Documentation

template<StatType T>
StatisticsPoint< T >::StatisticsPoint ( ) [inline]

Constructor sets sensible values.

References StatisticsPoint< T >::mirrorParticle, StatisticsPoint< T >::Position, and Vec3D::set_zero().

                          {
                this->Position.set_zero(); 
                mirrorParticle=-1;
                //~ this->set_zero(); 
        }
template<StatType T>
StatisticsPoint< T >::StatisticsPoint ( const StatisticsPoint< T > &  other) [inline]

Copy constructor; simply copies everything.

References StatisticsPoint< T >::mirrorParticle.

{*this = other; mirrorParticle=-1;}

Member Function Documentation

template<StatType T>
Mdouble StatisticsPoint< T >::CG_function ( Vec3D &  PI)

Returns the value of the course graining function phi(P,PI)

References Gaussian, HeavisideSphere, and polynomial.

                                                 {
        Mdouble dist2 = get_distance2(PI);
        if (get_CG_type()==HeavisideSphere) {
                return (get_w2()<dist2)?0.0:get_CG_invvolume();
        } else if (get_CG_type()==Gaussian) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume() * exp(-dist2/(2.0*get_w2()));
        } else if (get_CG_type()==polynomial) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume()*evaluatePolynomial(sqrt(dist2)/get_cutoff());
        } else { cerr << "error in CG_function" << endl; exit(-1); }
}
template<>
Mdouble StatisticsPoint< XY >::CG_function ( Vec3D &  PI) 
                                                             {
        return CG_function_2D(PI);
}
template<>
Mdouble StatisticsPoint< XZ >::CG_function ( Vec3D &  PI) 
                                                             {
        return CG_function_2D(PI);
}
template<>
Mdouble StatisticsPoint< YZ >::CG_function ( Vec3D &  PI) 
                                                             {
        return CG_function_2D(PI);
}
template<>
Mdouble StatisticsPoint< X >::CG_function ( Vec3D &  PI) 
                                                            {
        return CG_function_1D(PI);
}
template<>
Mdouble StatisticsPoint< Y >::CG_function ( Vec3D &  PI) 
                                                            {
        return CG_function_1D(PI);
}
template<>
Mdouble StatisticsPoint< Z >::CG_function ( Vec3D &  PI) 
                                                            {
        return CG_function_1D(PI);
}
template<>
double StatisticsPoint< O >::CG_function ( Vec3D &  ) 
                                                        {
        return get_CG_invvolume();
}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_function_1D ( Vec3D &  PI)

Returns the value of the course graining function phi(P,PI) averaged along a plane.

References Gaussian, HeavisideSphere, constants::pi, and polynomial.

                                                    {
        Mdouble dist2 = get_distance2(PI);
        if (get_CG_type()==HeavisideSphere) {
                return (get_w2()<dist2)?0.0:(get_CG_invvolume()*constants::pi*(get_w2()-dist2));
        } else if (get_CG_type()==Gaussian) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume() * exp(-dist2/(2.0*get_w2()));
        } else if (get_CG_type()==polynomial) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume()*evaluatePolynomial(sqrt(dist2)/get_cutoff());
        } else { cerr << "error in CG_function_1D" << endl; exit(-1); }
}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_function_2D ( Vec3D &  PI)

returns the value of the course graining function phi(P,PI) averaged along a line

Todo:
the volume should be calculated in set_CG_invvolume

References Gaussian, HeavisideSphere, and polynomial.

                                                    {
        Mdouble dist2 = get_distance2(PI);
        if (get_CG_type()==HeavisideSphere) {
                if (get_w2()<dist2) return 0.0;
                else {
                        Mdouble wn = sqrt(get_w2()-dist2);
                        return get_CG_invvolume()*2.0*wn; 
                        //return get_CG_invvolume()*(min(wn,gb->getBoundaryDistanceLeft()) +min(wn,gb->getBoundaryDistanceRight()));    
                }
        } else if (get_CG_type()==Gaussian) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume() * exp(-dist2/(2.0*get_w2()));
        } else if (get_CG_type()==polynomial) {
                return (get_cutoff2()<dist2)?0.0:get_CG_invvolume()*evaluatePolynomial(sqrt(dist2)/get_cutoff());
        } else { cerr << "error in CG_function_2D" << endl; exit(-1); }
}
template<StatType T>
Vec3D StatisticsPoint< T >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

gradient of phi

Todo:
{Only implemented for Gaussian}

References Gaussian.

                                                           {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return (P-Position)*(-phi/get_w2());
        else { cerr << "error in CG_gradient" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< YZ >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, Vec3D::Y, and Vec3D::Z.

                                                                       {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D(0.0,P.Y - Position.Y,P.Z - Position.Z)*(phi/get_w2());
        else { cerr << "error in CG_gradient<YZ>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< XZ >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, Vec3D::X, and Vec3D::Z.

                                                                       {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D(P.X - Position.X,0.0,P.Z - Position.Z)*(phi/get_w2());
        else { cerr << "error in CG_gradient<XZ>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< XY >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, Vec3D::X, and Vec3D::Y.

                                                                       {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D(P.X - Position.X,P.Y - Position.Y,0.0)*(phi/get_w2());
        else { cerr << "error in CG_gradient<XY>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< X >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, and Vec3D::X.

                                                                      {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D((P.X - Position.X)*(phi/get_w2()),0.0,0.0);
        else { cerr << "error in CG_gradient<X>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< Y >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, and Vec3D::Y.

                                                                      {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D(0.0,(P.Y - Position.Y)*(phi/get_w2()),0.0);
        else { cerr << "error in CG_gradient<Y>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< Z >::CG_gradient ( Vec3D &  P,
Mdouble  phi 
)

References Gaussian, and Vec3D::Z.

                                                                      {
        //CG_type_todo
        if (get_CG_type()==Gaussian) return Vec3D(0.0,0.0,(P.Z - Position.Z)*(phi/get_w2()));
        else { cerr << "error in CG_gradient<Z>" << endl; exit(-1); }
}
template<>
Vec3D StatisticsPoint< O >::CG_gradient ( Vec3D &  ,
double   
) 
{return Vec3D(0.0,0.0,0.0);}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
)

Returns the value of the coarse graining integral 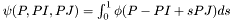$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $.

Todo:
Thomas: I think these static's are not necessary and dangerous (I think I put them there myself when I was young and stupid)

References Gaussian, Vec3D::GetLength(), HeavisideSphere, constants::pi, and polynomial.

{
        Vec3D P_P1 = Position - P1;
        Vec3D P_P2 = Position - P2;
        Mdouble a = dot(P_P1,P1_P2_normal);
        Mdouble b = dot(P_P2,P1_P2_normal);
        Vec3D tangential = P_P1 - a * P1_P2_normal;
        if (get_CG_type()==HeavisideSphere) {
                Mdouble wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) | (a*abs(a)>=wn2) | (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        Mdouble wn = sqrt(wn2);
                        return get_CG_invvolume()*( min(b,wn)-max(a,-wn) ) / P1_P2_distance;
                }
        } else if (get_CG_type()==Gaussian) { //Gaussian
                static Mdouble wsq2 = sqrt(2*get_w2());
                static Mdouble f = sqrt(2*constants::pi*get_w2());
                return get_CG_invvolume() * f * exp(-dot(tangential,tangential)/(2.0*get_w2()))
                        * (erf(b/wsq2)-erf(a/wsq2))/2/P1_P2_distance;
        } else if (get_CG_type()==polynomial) {
                double wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) | (a*abs(a)>=wn2) | (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        double wn = sqrt(wn2);
                        double w = get_w();
                        return get_CG_invvolume()*evaluateIntegral(max(a,-wn)/w,min(b,wn)/w,tangential.GetLength()/w)*w / P1_P2_distance;
                }
                //CG_type_todo
        } else { cerr << "error in CG_integral" << endl; exit(-1); }
}
template<>
Mdouble StatisticsPoint< XY >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                     {
        return CG_integral_2D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
Mdouble StatisticsPoint< XZ >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                     {
        return CG_integral_2D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
Mdouble StatisticsPoint< YZ >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                     {
        return CG_integral_2D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
Mdouble StatisticsPoint< X >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                    {
        return CG_integral_1D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
Mdouble StatisticsPoint< Y >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                    {
        return CG_integral_1D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
Mdouble StatisticsPoint< Z >::CG_integral ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
) 
                                                                                                                    {
        return CG_integral_1D(P1, P2, P1_P2_normal, P1_P2_distance);
}
template<>
double StatisticsPoint< O >::CG_integral ( Vec3D &  ,
Vec3D &  ,
Vec3D &  ,
double   
) 
                                                                                {
        return get_CG_invvolume();
}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_integral_1D ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
)

Returns the value of the coarse graining integral 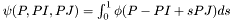$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $ averaged along a plane.

Todo:
Thomas: the following line has to be tested

References Gaussian, HeavisideSphere, constants::pi, polynomial, and sqr.

{

        Vec3D P_P1 = Position - P1;
        Vec3D P_P2 = Position - P2;
        Mdouble a = dot(P_P1,P1_P2_normal);
        Mdouble b = dot(P_P2,P1_P2_normal);
        Vec3D tangential = P_P1 - a * P1_P2_normal;

        if (get_CG_type()==HeavisideSphere) {
                Mdouble wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) | (a*abs(a)>=wn2) | (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        //if the normal is parallel to the averaging direction
                        if (max(abs(a),abs(b))<1e-20) {
                                return get_CG_invvolume() * constants::pi * wn2;
                        }
                        Mdouble wn = sqrt(wn2);
                        return get_CG_invvolume() / P1_P2_distance
                                *( ((b>= wn)?( 2.0/3.0*constants::pi*wn2*wn):(b*constants::pi*(wn2-sqr(b)/3.0)))
                                        -((a<=-wn)?(-2.0/3.0*constants::pi*wn2*wn):(a*constants::pi*(wn2-sqr(a)/3.0))) );
                }
        } else if (get_CG_type()==Gaussian) { //Gaussian
                if (P1_P2_distance<1e-20) { 
                        return get_CG_invvolume() * exp(-dot(P_P1,P_P1)/(2.0*get_w2()));
                }
                Mdouble wsq2 = sqrt(2*get_w2());
                Mdouble f = sqrt(2*constants::pi*get_w2());
                return get_CG_invvolume() * f * exp(-dot(tangential,tangential)/(2.0*get_w2()))
                        * (erf(b/wsq2)-erf(a/wsq2))/2/P1_P2_distance;
        } else if (get_CG_type()==polynomial) {
                double wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) | (a*abs(a)>=wn2) | (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        double wn = sqrt(wn2);
                        //if the normal is parallel to the averaging direction
                        if (max(abs(a),abs(b))<1e-20) {
                                return get_CG_invvolume() * 2 * wn;
                        }
                        double w = get_w();
                        return get_CG_invvolume()*evaluateIntegral(max(a,-wn)/w,min(b,wn)/w,dot(tangential,tangential)/w)*w / P1_P2_distance;
                }
        } else { cerr << "error in CG_integral_1D" << endl; exit(-1); }
}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_integral_2D ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
)

Returns the value of the coarse graining integral 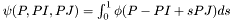$ \psi(P,PI,PJ) = \int_0^1 \phi(P - PI + s PJ) ds $ averaged along a line.

Todo:
Thomas: the following line has to be tested

References Gaussian, Vec3D::GetLength(), HeavisideSphere, constants::pi, polynomial, and sqr.

{
        Vec3D P_P1 = Position - P1;
        Vec3D P_P2 = Position - P2;
        Mdouble a = dot(P_P1,P1_P2_normal);
        Mdouble b = dot(P_P2,P1_P2_normal);
        Vec3D tangential = P_P1 - a * P1_P2_normal;
        if (get_CG_type()==HeavisideSphere) {
                Mdouble wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) || (a*abs(a)>=wn2) || (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        Mdouble wn = sqrt(wn2);
                        //if the normal is parallel to the averaging direction
                        if (max(abs(a),abs(b))<1e-20) {
                                return get_CG_invvolume() * 2 * wn;
                        }
                        return get_CG_invvolume() / P1_P2_distance
                                *( ((b>= wn)?(constants::pi*wn2/2.0):( b*sqrt(wn2-sqr(b))+wn2*asin(b/wn)))
                                        +((a<=-wn)?(constants::pi*wn2/2.0):(-a*sqrt(wn2-sqr(a))-wn2*asin(a/wn))));
                }
        } else if (get_CG_type()==Gaussian) { //Gaussian
                if (dot(P1_P2_normal,P1_P2_normal)<1e-20) { 
                        //cout << "!3";
                        //since we average parallel to the force line, the CG integral is shaped like the CG function
                        return get_CG_invvolume() * exp(-dot(P_P1,P_P1)/(2.0*get_w2()));
                }
                static Mdouble wsq2 = sqrt(2*get_w2());
                static Mdouble f = sqrt(2*constants::pi*get_w2());
                return get_CG_invvolume() * f * exp(-dot(tangential,tangential)/(2.0*get_w2()))
                        * (erf(b/wsq2)-erf(a/wsq2))/2/P1_P2_distance;
        } else if (get_CG_type()==polynomial) {
                double wn2 = get_w2() - dot(tangential,tangential);
                if ((wn2<=0) | (a*abs(a)>=wn2) | (b*abs(b)<=-wn2)) {
                        return 0;
                } else {
                        double wn = sqrt(wn2);
                        //if the normal is parallel to the averaging direction
                        if (max(abs(a),abs(b))<1e-20) return get_CG_invvolume() * 2 * wn;
                        double w = get_w();
                        return get_CG_invvolume()*evaluateIntegral(max(a,-wn)/w,min(b,wn)/w,tangential.GetLength()/w)*w / P1_P2_distance;
                }
                //CG_type_todo
        } else { cerr << "error in CG_integral_2D" << endl; exit(-1); }
}
template<StatType T>
Mdouble StatisticsPoint< T >::CG_integral_3D ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal,
Mdouble  P1_P2_distance 
)
template<StatType T>
Vec3D StatisticsPoint< T >::CG_integral_gradient ( Vec3D &  P1,
Vec3D &  P2,
Vec3D &  P1_P2_normal 
)

gradient of phi

Todo:
{Only implemented for Gaussian and statavg Z}

References Gaussian, constants::pi, and sqr.

                                                                                        {
        Vec3D P_P1 = Position - P1;
        Vec3D P_P2 = Position - P2;
        Mdouble a = dot(P_P1,P1_P2_normal);
        Mdouble b = dot(P_P2,P1_P2_normal);
        Vec3D tangential = P_P1 - a * P1_P2_normal;
        //CG_type_todo
        if (get_CG_type()==Gaussian) {
                Mdouble wsq2 = sqrt(2*get_w2());
                Mdouble f = sqrt(2*constants::pi*get_w2());
                return Vec3D(0.0,0.0,(exp(-sqr(a/wsq2))-exp(-sqr(b/wsq2)))/f/(P2.Z-P1.Z));
        } else { cerr << "error in CG_integral_gradient" << endl; exit(-1); }
        //~ if (get_CG_type()==Gaussian) return Vec3D(0.0,0.0,0.0);
        //~ else { cerr << "error in CG_function" << endl; exit(-1); }
}
template<StatType T>
Mdouble StatisticsPoint< T >::dot ( Vec3D &  P,
Vec3D &  Q 
)

Returns the dot product of two vectors in the coordinates that are not averaged about.

References Vec3D::X, Vec3D::Y, and Vec3D::Z.

                                                  {
        return P.X*Q.X + P.Y*Q.Y + P.Z*Q.Z;
}
template<>
Mdouble StatisticsPoint< XY >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::X, and Vec3D::Y.

{return P.X*Q.X + P.Y*Q.Y;}
template<>
Mdouble StatisticsPoint< XZ >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::X, and Vec3D::Z.

{return P.X*Q.X + P.Z*Q.Z;}
template<>
Mdouble StatisticsPoint< YZ >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::Y, and Vec3D::Z.

{return P.Y*Q.Y + P.Z*Q.Z;}
template<>
Mdouble StatisticsPoint< X >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::X.

{return P.X*Q.X;}
template<>
Mdouble StatisticsPoint< Y >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::Y.

{return P.Y*Q.Y;}
template<>
Mdouble StatisticsPoint< Z >::dot ( Vec3D &  P,
Vec3D &  Q 
)

References Vec3D::Z.

{return P.Z*Q.Z;}
template<>
double StatisticsPoint< O >::dot ( Vec3D &  ,
Vec3D &   
) 
{return 0;}
template<StatType T>
Mdouble StatisticsPoint< T >::evaluateIntegral ( Mdouble  n1,
Mdouble  n2,
Mdouble  t 
) [inline]

see StatisticsVector::evaluateIntegral

References StatisticsPoint< T >::gb.

{return gb->evaluateIntegral(n1,n2,t);}
template<StatType T>
Mdouble StatisticsPoint< T >::evaluatePolynomial ( Mdouble  r) [inline]

see StatisticsVector::evaluatePolynomial

References StatisticsPoint< T >::gb.

{return gb->evaluatePolynomial(r);}
template<StatType T>
Mdouble StatisticsPoint< T >::get_CG_invvolume ( ) [inline]

returns CG_invvolume

References StatisticsPoint< T >::CG_invvolume.

{return this->CG_invvolume;}
template<StatType T>
CG StatisticsPoint< T >::get_CG_type ( ) const [inline]

see StatisticsVector::get_CG_type

References StatisticsPoint< T >::gb.

{return this->gb->get_CG_type();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_cutoff ( ) [inline]

see StatisticsVector::get_cutoff

References StatisticsPoint< T >::gb.

{return this->gb->get_cutoff();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_cutoff2 ( ) [inline]

see StatisticsVector::get_cutoff2

References StatisticsPoint< T >::gb.

{return this->gb->get_cutoff2();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_distance2 ( Vec3D &  P)

returns the coarse graining distance in the coordinates that are not averaged about

References sqr, Vec3D::X, Vec3D::Y, and Vec3D::Z.

                                                  {
        return sqr(P.X-Position.X)+sqr(P.Y-Position.Y)+sqr(P.Z-Position.Z);
}
template<>
Mdouble StatisticsPoint< XY >::get_distance2 ( Vec3D &  P)

References sqr, Vec3D::X, and Vec3D::Y.

{return sqr(P.X-Position.X)+sqr(P.Y-Position.Y);}
template<>
Mdouble StatisticsPoint< XZ >::get_distance2 ( Vec3D &  P)

References sqr, Vec3D::X, and Vec3D::Z.

{return sqr(P.X-Position.X)+sqr(P.Z-Position.Z);}
template<>
Mdouble StatisticsPoint< YZ >::get_distance2 ( Vec3D &  P)

References sqr, Vec3D::Y, and Vec3D::Z.

{return sqr(P.Y-Position.Y)+sqr(P.Z-Position.Z);}
template<>
Mdouble StatisticsPoint< X >::get_distance2 ( Vec3D &  P)

References sqr, and Vec3D::X.

{return sqr(P.X-Position.X);}
template<>
Mdouble StatisticsPoint< Y >::get_distance2 ( Vec3D &  P)

References sqr, and Vec3D::Y.

{return sqr(P.Y-Position.Y);}
template<>
Mdouble StatisticsPoint< Z >::get_distance2 ( Vec3D &  P)

References sqr, and Vec3D::Z.

{return sqr(P.Z-Position.Z);}
template<>
double StatisticsPoint< O >::get_distance2 ( Vec3D &  ) 
{return 0;}
template<StatType T>
void StatisticsPoint< T >::get_n ( int &  nx_,
int &  ny_,
int &  nz_ 
) [inline]

see StatisticsVector::get_n

References StatisticsPoint< T >::gb.

{this->gb->get_n(nx_,ny_,nz_);}
template<StatType T>
Vec3D StatisticsPoint< T >::get_Position ( ) const [inline]

returns Position

References StatisticsPoint< T >::Position.

{return this->Position;}
template<StatType T>
Mdouble StatisticsPoint< T >::get_w ( ) const [inline]

see StatisticsVector::get_w

References StatisticsPoint< T >::gb.

{return this->gb->get_w();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_w2 ( ) const [inline]

see StatisticsVector::get_w2

References StatisticsPoint< T >::gb.

{return this->gb->get_w2();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_xmaxStat ( ) [inline]

see StatisticsVector::get_xmaxStat

References StatisticsPoint< T >::gb.

{return this->gb->get_xmaxStat();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_xminStat ( ) [inline]

see StatisticsVector::get_xminStat

References StatisticsPoint< T >::gb.

{return this->gb->get_xminStat();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_ymaxStat ( ) [inline]

see StatisticsVector::get_ymaxStat

References StatisticsPoint< T >::gb.

{return this->gb->get_ymaxStat();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_yminStat ( ) [inline]

see StatisticsVector::get_yminStat

References StatisticsPoint< T >::gb.

{return this->gb->get_yminStat();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_zmaxStat ( ) [inline]

see StatisticsVector::get_zmaxStat

References StatisticsPoint< T >::gb.

{return this->gb->get_zmaxStat();}
template<StatType T>
Mdouble StatisticsPoint< T >::get_zminStat ( ) [inline]

see StatisticsVector::get_zminStat

References StatisticsPoint< T >::gb.

{return this->gb->get_zminStat();}
template<StatType T>
StatisticsPoint< T > StatisticsPoint< T >::getSquared ( )

Squares all statistical variables; needed for variance.

References StatisticsPoint< T >::CollisionalHeatFlux, StatisticsPoint< T >::Density, StatisticsPoint< T >::Displacement, StatisticsPoint< T >::DisplacementMomentum, StatisticsPoint< T >::DisplacementMomentumFlux, StatisticsPoint< T >::Dissipation, StatisticsPoint< T >::EnergyFlux, StatisticsPoint< T >::Fabric, StatisticsPoint< T >::Momentum, StatisticsPoint< T >::MomentumFlux, StatisticsPoint< T >::NormalStress, StatisticsPoint< T >::NormalTraction, StatisticsPoint< T >::Nu, StatisticsPoint< T >::Potential, sqr, StatisticsPoint< T >::TangentialStress, and StatisticsPoint< T >::TangentialTraction.

                                                  {
        StatisticsPoint<T> P;
        P.Nu = sqr(Nu);
        P.Density = sqr(Density);
        P.Momentum = square(Momentum);
        P.DisplacementMomentum = square(DisplacementMomentum);
        P.Displacement = square(Displacement);
        P.MomentumFlux = square(MomentumFlux);
        P.DisplacementMomentumFlux = square(DisplacementMomentumFlux);
        P.EnergyFlux = square(EnergyFlux);
        P.NormalStress = square(NormalStress);
        P.TangentialStress = square(TangentialStress);
        P.NormalTraction = square(NormalTraction);
        P.TangentialTraction = square(TangentialTraction);
        P.Fabric = square(Fabric);
        P.CollisionalHeatFlux = square(CollisionalHeatFlux);
        P.Dissipation = sqr(Dissipation);
        P.Potential = sqr(Potential);
        return P;
}
template<StatType T>
StatisticsPoint< T > & StatisticsPoint< T >::operator+= ( const StatisticsPoint< T > &  P) [inline]

Defines a plus operator needed to average values ( 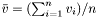$ \bar{v} = (\sum_{i=1}^n v_i)/n $ )

References StatisticsPoint< T >::CollisionalHeatFlux, StatisticsPoint< T >::Density, StatisticsPoint< T >::Displacement, StatisticsPoint< T >::DisplacementMomentum, StatisticsPoint< T >::DisplacementMomentumFlux, StatisticsPoint< T >::Dissipation, StatisticsPoint< T >::EnergyFlux, StatisticsPoint< T >::Fabric, StatisticsPoint< T >::Momentum, StatisticsPoint< T >::MomentumFlux, StatisticsPoint< T >::NormalStress, StatisticsPoint< T >::NormalTraction, StatisticsPoint< T >::Nu, StatisticsPoint< T >::Potential, StatisticsPoint< T >::TangentialStress, and StatisticsPoint< T >::TangentialTraction.

{
        Nu += P.Nu;
        Density += P.Density;
        Momentum += P.Momentum;
        DisplacementMomentum += P.DisplacementMomentum;
        Displacement += P.Displacement;
        MomentumFlux += P.MomentumFlux;
        DisplacementMomentumFlux += P.DisplacementMomentumFlux;
        EnergyFlux += P.EnergyFlux;
        NormalStress += P.NormalStress;
        TangentialStress += P.TangentialStress;
        NormalTraction += P.NormalTraction;
        TangentialTraction += P.TangentialTraction;
        Fabric += P.Fabric;
        CollisionalHeatFlux += P.CollisionalHeatFlux;
        Dissipation += P.Dissipation;
        Potential += P.Potential;
        return *this;
}
template<StatType T>
StatisticsPoint< T > & StatisticsPoint< T >::operator-= ( const StatisticsPoint< T > &  P) [inline]

Defines a plus operator needed to calculate variance.

References StatisticsPoint< T >::CollisionalHeatFlux, StatisticsPoint< T >::Density, StatisticsPoint< T >::Displacement, StatisticsPoint< T >::DisplacementMomentum, StatisticsPoint< T >::DisplacementMomentumFlux, StatisticsPoint< T >::Dissipation, StatisticsPoint< T >::EnergyFlux, StatisticsPoint< T >::Fabric, StatisticsPoint< T >::Momentum, StatisticsPoint< T >::MomentumFlux, StatisticsPoint< T >::NormalStress, StatisticsPoint< T >::NormalTraction, StatisticsPoint< T >::Nu, StatisticsPoint< T >::Potential, StatisticsPoint< T >::TangentialStress, and StatisticsPoint< T >::TangentialTraction.

{
        Nu -= P.Nu;
        Density -= P.Density;
        Momentum -= P.Momentum;
        DisplacementMomentum -= P.DisplacementMomentum;
        Displacement -= P.Displacement;
        MomentumFlux -= P.MomentumFlux;
        DisplacementMomentumFlux -= P.DisplacementMomentumFlux;
        EnergyFlux -= P.EnergyFlux;
        NormalStress -= P.NormalStress;
        TangentialStress -= P.TangentialStress;
        NormalTraction -= P.NormalTraction;
        TangentialTraction -= P.TangentialTraction;
        Fabric -= P.Fabric;
        CollisionalHeatFlux -= P.CollisionalHeatFlux;
        Dissipation -= P.Dissipation;
        Potential -= P.Potential;
        return *this;
}
template<StatType T>
StatisticsPoint< T > & StatisticsPoint< T >::operator/= ( const Mdouble  a) [inline]

Defines a division operator needed to average values ( 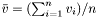$ \bar{v} = (\sum_{i=1}^n v_i)/n $ ) 

{
        Nu /= a;
        Density /= a;
        Momentum /= a;
        DisplacementMomentum /= a;
        Displacement /= a;
        MomentumFlux /= a;
        DisplacementMomentumFlux /= a;
        EnergyFlux /= a;
        NormalStress /= a;
        TangentialStress /= a;
        NormalTraction /= a;
        TangentialTraction /= a;
        Fabric /= a;
        CollisionalHeatFlux /= a;
        Dissipation /= a;
        Potential /= a;
        return *this;
}
template<StatType T>
StatisticsPoint< T > & StatisticsPoint< T >::operator= ( const StatisticsPoint< T > &  P) [inline]

Defines a equal operator needed for copy constructor.

References StatisticsPoint< T >::CollisionalHeatFlux, StatisticsPoint< T >::Density, StatisticsPoint< T >::Displacement, StatisticsPoint< T >::DisplacementMomentum, StatisticsPoint< T >::DisplacementMomentumFlux, StatisticsPoint< T >::Dissipation, StatisticsPoint< T >::EnergyFlux, StatisticsPoint< T >::Fabric, StatisticsPoint< T >::Momentum, StatisticsPoint< T >::MomentumFlux, StatisticsPoint< T >::NormalStress, StatisticsPoint< T >::NormalTraction, StatisticsPoint< T >::Nu, StatisticsPoint< T >::Potential, StatisticsPoint< T >::TangentialStress, and StatisticsPoint< T >::TangentialTraction.

{
        Nu = P.Nu;
        Density = P.Density;
        Momentum = P.Momentum;
        DisplacementMomentum = P.DisplacementMomentum;
        Displacement = P.Displacement;
        MomentumFlux = P.MomentumFlux;
        DisplacementMomentumFlux = P.DisplacementMomentumFlux;
        EnergyFlux = P.EnergyFlux;
        NormalStress = P.NormalStress;
        TangentialStress = P.TangentialStress;
        NormalTraction = P.NormalTraction;
        TangentialTraction = P.TangentialTraction;
        Fabric = P.Fabric;
        CollisionalHeatFlux = P.CollisionalHeatFlux;
        Dissipation = P.Dissipation;
        Potential = P.Potential;
        return *this;
}
template<StatType T>
string StatisticsPoint< T >::print ( ) const

Outputs statistical variables in human-readable format.

Referenced by StatisticsVector< T >::write_time_average_statistics().

{
        stringstream ss;
        ss<< "Nu " << Nu
                <<", Density " << Density 
                << ",\n Momentum " << Momentum
                << ",\n DisplacementMomentum " << DisplacementMomentum
                << ",\n Displacement " << Displacement
                << ",\n MomentumFlux " << MomentumFlux
                << ",\n DisplacementMomentumFlux " << DisplacementMomentumFlux
                << ",\n EnergyFlux " << EnergyFlux
                << ",\n NormalStress " << NormalStress  
                << ",\n TangentialStress " << TangentialStress
                << ",\n NormalTraction " << NormalTraction  
                << ",\n TangentialTraction " << TangentialTraction
                << ",\n Fabric " << Fabric
                << ",\n CollisionalHeatFlux " << CollisionalHeatFlux
                << ",\n Dissipation " << Dissipation
                << ",\n Potential " << Potential;
        return ss.str();
}
template<StatType T>
string StatisticsPoint< T >::print_sqrt ( ) const

Outputs root of statistical variables in human-readable format. 

{
        stringstream ss;
        ss<< "Nu " << sqrt(Nu)
                << ", Density " << sqrt(Density)
                << ", Momentum " << sqrt(Momentum)
                << ", DisplacementMomentum " << sqrt(DisplacementMomentum)
                << ", Displacement " << sqrt(Displacement)
                << ", MomentumFlux " << sqrt(MomentumFlux)
                << ", DisplacementMomentumFlux " << sqrt(DisplacementMomentumFlux)
                << ", EnergyFlux " << sqrt(EnergyFlux)
                << ", NormalStress " << sqrt(NormalStress)
                << ", TangentialStress " << sqrt(TangentialStress)
                << ", NormalTraction " << sqrt(NormalTraction)
                << ", TangentialTraction " << sqrt(TangentialTraction)
                << ", Fabric " << sqrt(Fabric)
                << ", CollisionalHeatFlux " << sqrt(CollisionalHeatFlux)
                << ", Dissipation " << sqrt(Dissipation)
                << ", Potential " << sqrt(Potential);
        return ss.str();
}
template<StatType T>
void StatisticsPoint< T >::set_CG_invvolume ( )

sets CG_invvolume

template<>
void StatisticsPoint< XYZ >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                            {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(gb->get_dim_particle());
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(3);
        } else { cerr << "error in CG_function" << endl; exit(-1); }
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_xmaxStat()-Position.X,Position.X-get_xminStat());
                //~ correct_dimension_for_bounded_domain(get_ymaxStat()-Position.Y,Position.Y-get_yminStat());
                //~ ///Should this be get_dim instead of get_dim_particle?
                //~ if (gb->get_dim_particle()==3) correct_dimension_for_bounded_domain(get_zmaxStat()-Position.Z,Position.Z-get_zminStat());
        //~ }
}
template<>
void StatisticsPoint< XY >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                           {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(2);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(2);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        if (gb->get_dim_particle()==3) CG_invvolume /= get_zmaxStat()-get_zminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_xmaxStat()-Position.X,Position.X-get_xminStat());
                //~ correct_dimension_for_bounded_domain(get_ymaxStat()-Position.Y,Position.Y-get_yminStat());
        //~ }
}
template<>
void StatisticsPoint< XZ >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                           {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(gb->get_dim_particle()-1);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(gb->get_dim_particle()-1);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        CG_invvolume /= get_ymaxStat()-get_yminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_xmaxStat()-Position.X,Position.X-get_xminStat());
                //~ if (gb->get_dim_particle()==3) correct_dimension_for_bounded_domain(get_zmaxStat()-Position.Z,Position.Z-get_zminStat());
        //~ }
}
template<>
void StatisticsPoint< YZ >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                           {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(gb->get_dim_particle()-1);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(gb->get_dim_particle()-1);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        CG_invvolume /= get_xmaxStat()-get_xminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_ymaxStat()-Position.Y,Position.Y-get_yminStat());
                //~ if (gb->get_dim_particle()==3) correct_dimension_for_bounded_domain(get_zmaxStat()-Position.Z,Position.Z-get_zminStat());
        //~ }
}
template<>
void StatisticsPoint< X >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                          {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(1);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(1);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        CG_invvolume /= get_ymaxStat()-get_yminStat();
        if (gb->get_dim_particle()==3) CG_invvolume /= get_zmaxStat()-get_zminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_xmaxStat()-Position.X,Position.X-get_xminStat());
        //~ }
}
template<>
void StatisticsPoint< Y >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                          {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(1);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(1);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        CG_invvolume /= get_xmaxStat()-get_xminStat();
        if (gb->get_dim_particle()==3) CG_invvolume /= get_zmaxStat()-get_zminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ correct_dimension_for_bounded_domain(get_ymaxStat()-Position.Y,Position.Y-get_yminStat());
        //~ }
}
template<>
void StatisticsPoint< Z >::set_CG_invvolume ( )

References Gaussian, HeavisideSphere, and polynomial.

                                          {
        if (get_CG_type()==HeavisideSphere) {
                set_Heaviside_invvolume();
        } else if (get_CG_type()==Gaussian) {
                set_Gaussian_invvolume(gb->get_dim_particle()-2);
        } else if (get_CG_type()==polynomial) {
                set_Polynomial_invvolume(gb->get_dim_particle()-2);
        } else { cerr << "error in set_CG_invvolume" << endl; exit(-1); }
        CG_invvolume /= get_xmaxStat()-get_xminStat();
        CG_invvolume /= get_ymaxStat()-get_yminStat();
        //~ if (gb->get_boundedDomain()) {
                //~ if (gb->get_dim_particle()==3) correct_dimension_for_bounded_domain(get_zmaxStat()-Position.Z,Position.Z-get_zminStat());
        //~ }
}
template<>
void StatisticsPoint< O >::set_CG_invvolume ( ) 
                                          {
        CG_invvolume = 1.0;
        CG_invvolume /= get_xmaxStat()-get_xminStat();
        CG_invvolume /= get_ymaxStat()-get_yminStat();
        if (gb->get_dim_particle()==3) CG_invvolume /= get_zmaxStat()-get_zminStat();
}
template<StatType T>
void StatisticsPoint< T >::set_CG_type ( const char *  CG_type) [inline]

see StatisticsVector::set_CG_type

References StatisticsPoint< T >::gb.

{this->gb->set_CG_type(CG_type);}
template<StatType T>
void StatisticsPoint< T >::set_Gaussian_invvolume ( int  dim)

sets CG_invvolume if CG_type=Gaussian

References cubic, constants::pi, and sqr.

                                                       {
        //this is the prefactor 1/V of phi(r)=1/V*exp(-|r|^2/w^2)
        CG_invvolume = 1/sqrt(2*constants::pi*get_w2());
        //here we take into account the cutoff radius
        CG_invvolume /= (erf(get_cutoff()/get_w()/sqrt(2)));
        if (dim==3) CG_invvolume = cubic(CG_invvolume);
        else if (dim==2) CG_invvolume = sqr(CG_invvolume);
        else if (dim==0) CG_invvolume = 1.;
}
template<StatType T>
static void StatisticsPoint< T >::set_gb ( StatisticsVector< T > *  new_gb) [inline, static]

see StatisticsVector::set_CG_type

References StatisticsPoint< T >::gb.

Referenced by StatisticsVector< T >::constructor().

{gb = new_gb;}
template<StatType T>
void StatisticsPoint< T >::set_Heaviside_invvolume ( )

sets CG_invvolume if CG_type=HeaviSideSphere

Todo:
{Thomas: check 2d case}

References constants::pi.

                                                 {
        CG_invvolume = 1.0/(4.0/3.0*constants::pi*sqrt(get_w2())*get_w2()); 
}
template<StatType T>
void StatisticsPoint< T >::set_Polynomial_invvolume ( int  dim)

sets CG_invvolume if CG_type=Polynomial 

                                                         {
        if (dim==3) CG_invvolume = 1.0/(sqrt(get_w2())*get_w2()); 
        else if (dim==2) CG_invvolume = 1.0/get_w2(); 
        else CG_invvolume = 1.0/sqrt(get_w2()); 
}
template<StatType T>
void StatisticsPoint< T >::set_Position ( Vec3D  new_) [inline]

sets Position

References StatisticsPoint< T >::Position.

{this->Position = new_;}
template<StatType T>
void StatisticsPoint< T >::set_w2 ( Mdouble  new_) [inline]

see StatisticsVector::set_w2

References StatisticsPoint< T >::gb.

{this->gb->set_w2(new_);}
template<StatType T>
void StatisticsPoint< T >::set_zero ( )

Sets all statistical variables to zero.

Referenced by StatisticsVector< T >::average().

                                  {
        Nu = 0.0;
        Density = 0.0;
        Momentum.set_zero();
        DisplacementMomentum.set_zero();
        Displacement.set_zero();
        MomentumFlux.set_zero();
        DisplacementMomentumFlux.set_zero();
        EnergyFlux.set_zero();
        TangentialStress.set_zero();
        NormalStress.set_zero();
        TangentialStress.set_zero();
        NormalTraction.set_zero();
        TangentialTraction.set_zero();
        Fabric.set_zero();
        CollisionalHeatFlux.set_zero();
        Dissipation = 0.0;
        Potential = 0.0;
}
template<StatType T>
void StatisticsPoint< T >::timeAverage ( const int  n) [inline]

Defines a division operator needed to time-average values (because the displacement does not have a value at the first timestep, this is slightly different than /=) 

                                                {
        Nu /= n;
        Density /= n;
        Momentum /= n;
        if (n==1) {
                DisplacementMomentum.set_zero();
                Displacement.set_zero();
                DisplacementMomentumFlux.set_zero();
        } else {
                DisplacementMomentum /= n-1;
                Displacement /= n-1;
                DisplacementMomentumFlux /= n-1;
        }
        MomentumFlux /= n;
        EnergyFlux /= n;
        NormalStress /= n;
        TangentialStress /= n;
        NormalTraction /= n;
        TangentialTraction /= n;
        Fabric /= n;
        CollisionalHeatFlux /= n;
        Dissipation /= n;
        Potential /= n;
        //~ cout << "Timeavg" << "z=" << Position.Z << ", n=" << n << ", Mz=" << Momentum.Z << ", DMz" << DisplacementMomentum.Z << endl;
}
template<StatType T>
string StatisticsPoint< T >::write ( ) const

Outputs statistical variables in computer-readable format. 

{
        stringstream ss;
        ss.precision(16);
        ss<< Nu
                << " " << Density
                << " " << Momentum
                << " " << DisplacementMomentum
                << " " << Displacement
                << " " << MomentumFlux
                << " " << DisplacementMomentumFlux
                << " " << EnergyFlux
                << " " << NormalStress  
                << " " << TangentialStress
                << " " << NormalTraction  
                << " " << TangentialTraction
                << " " << Fabric
                << " " << CollisionalHeatFlux
                << " " << Dissipation
                << " " << Potential;
        return ss.str();
}
template<StatType T>
string StatisticsPoint< T >::write_variable_names ( )

Outputs names of statistical variables in computer-readable format. 

                                                {
        stringstream ss;
        ss<< "Nu "
                << "Density "
                << "MomentumX "
                << "MomentumY "
                << "MomentumZ "
                << "DisplacementMomentumX "
                << "DisplacementMomentumY "
                << "DisplacementMomentumZ "
                << "DisplacementXX "
                << "DisplacementXY "
                << "DisplacementXZ "
                << "DisplacementYY "
                << "DisplacementYZ "
                << "DisplacementZZ "
                << "MomentumFluxXX "
                << "MomentumFluxXY "
                << "MomentumFluxXZ "
                << "MomentumFluxYY "
                << "MomentumFluxYZ "
                << "MomentumFluxZZ "
                << "DisplacementMomentumFluxXX "
                << "DisplacementMomentumFluxXY "
                << "DisplacementMomentumFluxXZ "
                << "DisplacementMomentumFluxYY "
                << "DisplacementMomentumFluxYZ "
                << "DisplacementMomentumFluxZZ "
                << "EnergyFluxX "
                << "EnergyFluxY "
                << "EnergyFluxZ "
                << "NormalStressXX "
                << "NormalStressXY "
                << "NormalStressXZ "
                << "NormalStressYX "
                << "NormalStressYY "
                << "NormalStressYZ "
                << "NormalStressZX "
                << "NormalStressZY "
                << "NormalStressZZ "
                << "TangentialStressXX "
                << "TangentialStressXY "
                << "TangentialStressXZ "
                << "TangentialStressYX "
                << "TangentialStressYY "
                << "TangentialStressYZ "
                << "TangentialStressZX "
                << "TangentialStressZY "
                << "TangentialStressZZ "
                << "NormalTractionX "
                << "NormalTractionY "
                << "NormalTractionZ "
                << "TangentialTractionX "
                << "TangentialTractionY "
                << "TangentialTractionZ "
                << "FabricXX "
                << "FabricXY "
                << "FabricXZ "
                << "FabricYY "
                << "FabricYZ "
                << "FabricZZ "
                << "CollisionalHeatFluxX "
                << "CollisionalHeatFluxY "
                << "CollisionalHeatFluxZ "
                << "Dissipation "
                << "Potential ";
        return ss.str();
}

Friends And Related Function Documentation

template<StatType T>
std::ostream& operator ( std::ostream &  os,
const StatisticsPoint< T > &  stat 
) [friend]

Outputs statistical variables to ostream.

Member Data Documentation

template<StatType T>
Mdouble StatisticsPoint< T >::CG_invvolume

Prefactor of CG function which depends on $w.

Referenced by StatisticsPoint< T >::get_CG_invvolume().

template<StatType T>
Vec3D StatisticsPoint< T >::CollisionalHeatFlux

Heat flux from collisions, 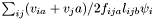$\sum_{ij} (v_{ia}+v_ja)/2 f_{ija} l_{ijb} \psi_i$.

Todo:
{Heat flux calculations have not been checked, only implemented}

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Mdouble StatisticsPoint< T >::Density

Density, 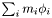$\sum_i m_i \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
MatrixSymmetric3D StatisticsPoint< T >::Displacement

Linear displacement, 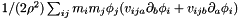$1/(2 \rho^2) \sum_{ij} m_i m_j \phi_j (v_{ija} \partial_b \phi_i + v_{ijb} \partial_a \phi_i) $.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Vec3D StatisticsPoint< T >::DisplacementMomentum

Momentum from linear displacement, 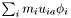$\sum_i m_i u_{ia} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
MatrixSymmetric3D StatisticsPoint< T >::DisplacementMomentumFlux

Momentum flux from linear displacement, 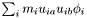$\sum_i m_i u_{ia} u_{ib} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Mdouble StatisticsPoint< T >::Dissipation

Dissipation form collisions, 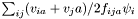$\sum_{ij} (v_{ia}+v_ja)/2 f_{ija} \psi_i$.

Todo:
{Dissipation calculations have not been checked, only implemented}

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Vec3D StatisticsPoint< T >::EnergyFlux

Energy flux, 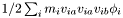$1/2 \sum_i m_i v_{ia} v_{ia} v_{ib} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
MatrixSymmetric3D StatisticsPoint< T >::Fabric

Fabric tensor, 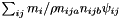$\sum_{ij} m_i/\rho n_{ija} n_{ijb} \psi_{ij}$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
StatisticsVector< T > * StatisticsPoint< T >::gb [static, private]

Pointer to StatisticsVector (to obtain global parameters)

Referenced by StatisticsPoint< T >::evaluateIntegral(), StatisticsPoint< T >::evaluatePolynomial(), StatisticsPoint< T >::get_CG_type(), StatisticsPoint< T >::get_cutoff(), StatisticsPoint< T >::get_cutoff2(), StatisticsPoint< T >::get_n(), StatisticsPoint< T >::get_w(), StatisticsPoint< T >::get_w2(), StatisticsPoint< T >::get_xmaxStat(), StatisticsPoint< T >::get_xminStat(), StatisticsPoint< T >::get_ymaxStat(), StatisticsPoint< T >::get_yminStat(), StatisticsPoint< T >::get_zmaxStat(), StatisticsPoint< T >::get_zminStat(), StatisticsPoint< T >::set_CG_type(), StatisticsPoint< T >::set_gb(), and StatisticsPoint< T >::set_w2().

template<StatType T>
int StatisticsPoint< T >::mirrorParticle

indicates that a position is a (fake) particles used for periodic walls

Referenced by StatisticsPoint< T >::StatisticsPoint().

template<StatType T>
Vec3D StatisticsPoint< T >::Momentum

Momentum, 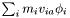$\sum_i m_i v_{ia} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
MatrixSymmetric3D StatisticsPoint< T >::MomentumFlux

Momentum flux, 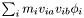$\sum_i m_i v_{ia} v_{ib} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Matrix3D StatisticsPoint< T >::NormalStress

Stress from normal forces, 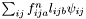$\sum_{ij} f^n_{ija} l_{ijb} \psi_{ij}$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Vec3D StatisticsPoint< T >::NormalTraction

Traction from normal forces, 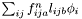$\sum_{ij} f^n_{ija} l_{ijb} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Mdouble StatisticsPoint< T >::Nu

Particle volume fraction, 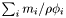$\sum_i m_i/\rho \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Vec3D StatisticsPoint< T >::Position [private]

Position at which evaluation occurs.

Referenced by StatisticsPoint< T >::get_Position(), StatisticsPoint< T >::set_Position(), and StatisticsPoint< T >::StatisticsPoint().

template<StatType T>
Mdouble StatisticsPoint< T >::Potential

Elastic energy 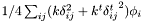$1/4 \sum_{ij} (k \delta_{ij}^2 +k^t {\delta^t_{ij}}^2) \phi_i$.

Todo:
{Potential calculations have not been checked, only implemented; fstat file does not include the torsional and rolling spring and hence cannot account for their potential}

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Matrix3D StatisticsPoint< T >::TangentialStress

Stress from tangential forces, 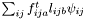$\sum_{ij} f^t_{ija} l_{ijb} \psi_{ij}$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

template<StatType T>
Vec3D StatisticsPoint< T >::TangentialTraction

Traction from tangential forces, 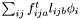$\sum_{ij} f^t_{ija} l_{ijb} \phi_i$.

Referenced by StatisticsPoint< T >::getSquared(), StatisticsPoint< T >::operator+=(), StatisticsPoint< T >::operator-=(), and StatisticsPoint< T >::operator=().

The documentation for this struct was generated from the following files:
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines
Generated on Wed Apr 17 2013 13:05:09 for HG-MD by   doxygen 1.7.6.1